Category Theory via C# (2) Monoid
[LINQ via C# series]
[Category Theory via C# series]
Latest version: https://weblogs.asp.net/dixin/category-theory-via-csharp-2-monoid
Monoid and monoid laws
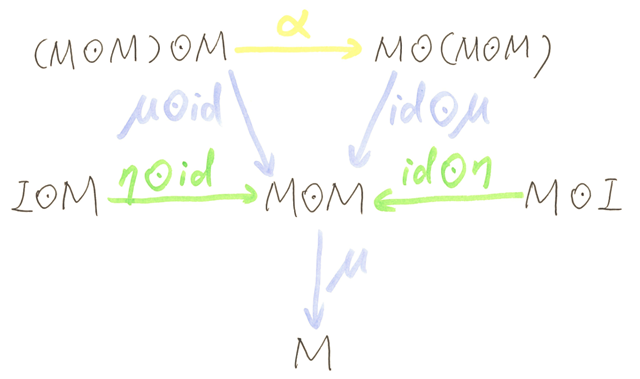
A monoid, denoted a 3-tuple (M, ⊙, I), is a set M with
- a binary operator ⊙ : M ⊙ M → M
- This operation M ⊙ M → M is denoted μ
- and a special element unit, denoted I, I ∈ M
- I → M is denoted η
satisfying:
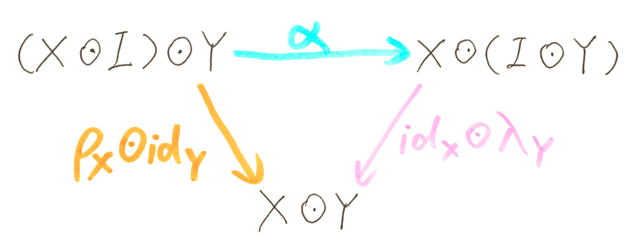
- left unit law λX: I ⊙ X ≌ X
- right unit law ρX: X ≌ X ⊙ I
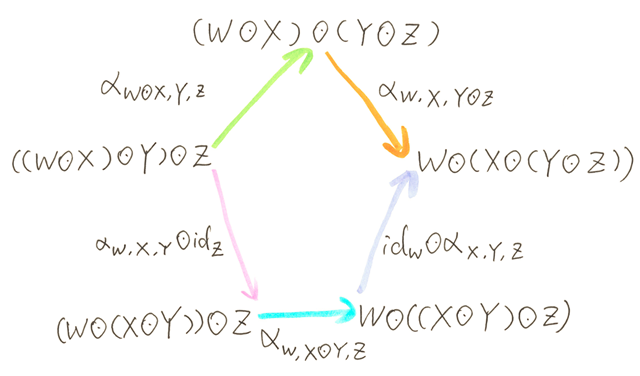
- associative law αX, Y, Z: (X ⊙ Y) ⊙ Z ≌ X ⊙ (Y ⊙ Z)
so that:
This is quite general and abstract. A intuitive example is the set of all integers, with operator + and unit 0. So this 3-tuple (integer, +, 0) satisfies:
- 0 + x ≌ x
- x ≌ x + 0
- (x + y) + z ≌ x + (y + z)
where x, y, z are elements of the set of integers. Therefore (integer, +, 0) is a monoid.
A monoid can be represented in C# as:
public partial interface IMonoid<T> { T Unit { [Pure] get; } Func<T, T, T> Binary { [Pure] get; } }
A default implementation is straight forward:
public partial class Monoid<T> : IMonoid<T> { public Monoid(T unit, [Pure] Func<T, T, T> binary) { this.Unit = unit; this.Binary = binary; } public T Unit { [Pure] get; } public Func<T, T, T> Binary { [Pure] get; } }
C#/.NET monoids
First of all, an extension method is created for convenience:
[Pure] public static class MonoidExtensions { public static IMonoid<T> Monoid<T>(this T unit, Func<T, T, T> binary) { return new Monoid<T>(unit, binary); } }
Void and Unit monoids
Theoretically System.Void can be a monoid. Its source code is:
public struct Void { }
which leads to only one way to get the Void value:
Void value = new Void();
So a monoid can be constructed as:
IMonoid<Void> voidMonoid = new Void().Monoid((a, b) => new Void());
However, C# compiler does not allow System.Void to be used like this. There are 2 workarounds:
- Copy above Void definition to local
- Use Microsoft.FSharp.Core.Unit to replace System.Void
F#’s unit is equivalent to C#’s void, and Microsoft.FSharp.Core.Unit is semantically close to System.Void. Unit’s source code is:
type Unit() = override x.GetHashCode() = 0 override x.Equals(obj:obj) = match obj with null -> true | :? Unit -> true | _ -> false interface System.IComparable with member x.CompareTo(_obj:obj) = 0 and unit = Unit
The difference is, Unit is a class, and its only possible value is null.
Unit unit = null;
So a monoid can be constructed by Unit too:
IMonoid<Unit> unitMonoid = ((Unit)null).Monoid((a, b) => null);
More examples
As fore mentioned, (int, +, 0) is a monoid:
IMonoid<int> addInt32 = 0.Monoid((a, b) => a + b); Assert.AreEqual(0, addInt32.Unit); Assert.AreEqual(1 + 2, addInt32.Binary(1, 2)); // Monoid law 1: Unit Binary m == m Assert.AreEqual(1, addInt32.Binary(addInt32.Unit, 1)); // Monoid law 2: m Binary Unit == m Assert.AreEqual(1, addInt32.Binary(1, addInt32.Unit)); // Monoid law 3: (m1 Binary m2) Binary m3 == m1 Binary (m2 Binary m3) Assert.AreEqual(addInt32.Binary(addInt32.Binary(1, 2), 3), addInt32.Binary(1, addInt32.Binary(2, 3)));
Brian Beckman had a clock monoid in a video - consider numbers on the clock:
If a ⊙ b is defined as a => b => (a + b) % 12, then 12 becomes the unit. So:
IMonoid<int> clock = 12.Monoid((a, b) => (a + b) % 12);
Here are more similar examples:
- (int, *, 1)
- (string, string.Concat, string.Empty)
- (bool, ||, false)
- (bool, &&, true)
- (IEnumerable<T>, Enumerable.Concat, Enumerable.Empty<T>())
Nullable<T> monoid
And monoid (Nullable<T>, ⊙, I) is interesting.
First of all, the built-in System.Nullable<> only works for value type, since reference type can naturally be null. Here for the category theory discussion, a Nullable<T> for any type can be reinvented:
public class Nullable<T> { private readonly Lazy<Tuple<bool, T>> factory; public Nullable(Func<Tuple<bool, T>> factory = null) { this.factory = factory == null ? null : new Lazy<Tuple<bool, T>>(factory); } public bool HasValue { [Pure] get { return this.factory?.Value != null && this.factory.Value.Item1 && this.factory.Value.Item2 != null; } } public T Value { [Pure] get { // Message is copied from mscorlib.dll string table, where key is InvalidOperation_NoValue. Contract.Requires<InvalidOperationException>(this.HasValue, "Nullable object must have a value."); return this.factory.Value.Item2; } } }
This Nullable<T>’s constructor takes a factory function which returns a tuple of bool and T value:
- When factory function is not provided (null), Nullable<T> does not have value.
- When factory function is provided, the function returns a tuple if executed.
- The tuple’s bool value indicates there is a value available (because when T is a value type, the other item in the tuple cannot be null).
- When the bool is true and the other T value is not null, Nullable<T> has a value.
Below is one way to define the binary operator ⊙, taking new Nullable<T>() - a Nullable<T> has no value - as the unit:
[Pure] public static partial class MonoidExtensions { public static IMonoid<T> Monoid<T> (this T unit, Func<T, T, T> binary) => new Monoid<T>(unit, binary); public static IMonoid<Nullable<TSource>> MonoidOfNullable<TSource> (this IMonoid<TSource> monoid) => new Monoid<Nullable<TSource>>( new Nullable<TSource>(), (a, b) => new Nullable<TSource>(() => { if (a.HasValue && b.HasValue) { return Tuple.Create(true, monoid.Binary(a.Value, b.Value)); } if (a.HasValue) { return Tuple.Create(true, a.Value); } if (b.HasValue) { return Tuple.Create(true, b.Value); } return Tuple.Create(false, default(TSource)); })); }
So that (Nullable<T>, ⊙, Nullable<T>()) becomes a monoid.
Unit tests
These unit tests demonstrate how the monoids are constructed and how the monoid laws are satisfied:
[TestClass] public class MonoidTests { [TestMethod()] public void StringTest() { IMonoid<string> concatString = string.Empty.Monoid((a, b) => string.Concat(a, b)); Assert.AreEqual(string.Empty, concatString.Unit); Assert.AreEqual("ab", concatString.Binary("a", "b")); // Monoid law 1: Unit Binary m == m Assert.AreEqual("ab", concatString.Binary(concatString.Unit, "ab")); // Monoid law 2: m Binary Unit == m Assert.AreEqual("ab", concatString.Binary("ab", concatString.Unit)); // Monoid law 3: (m1 Binary m2) Binary m3 == m1 Binary (m2 Binary m3) Assert.AreEqual(concatString.Binary(concatString.Binary("a", "b"), "c"), concatString.Binary("a", concatString.Binary("b", "c"))); } [TestMethod()] public void Int32Test() { IMonoid<int> addInt32 = 0.Monoid((a, b) => a + b); Assert.AreEqual(0, addInt32.Unit); Assert.AreEqual(1 + 2, addInt32.Binary(1, 2)); // Monoid law 1: Unit Binary m == m Assert.AreEqual(1, addInt32.Binary(addInt32.Unit, 1)); // Monoid law 2: m Binary Unit == m Assert.AreEqual(1, addInt32.Binary(1, addInt32.Unit)); // Monoid law 3: (m1 Binary m2) Binary m3 == m1 Binary (m2 Binary m3) Assert.AreEqual(addInt32.Binary(addInt32.Binary(1, 2), 3), addInt32.Binary(1, addInt32.Binary(2, 3))); IMonoid<int> multiplyInt32 = 1.Monoid((a, b) => a * b); Assert.AreEqual(1, multiplyInt32.Unit); Assert.AreEqual(1 * 2, multiplyInt32.Binary(1, 2)); // Monoid law 1: Unit Binary m == m Assert.AreEqual(2, multiplyInt32.Binary(multiplyInt32.Unit, 2)); // Monoid law 2: m Binary Unit == m Assert.AreEqual(2, multiplyInt32.Binary(2, multiplyInt32.Unit)); // Monoid law 3: (m1 Binary m2) Binary m3 == m1 Binary (m2 Binary m3) Assert.AreEqual(multiplyInt32.Binary(multiplyInt32.Binary(1, 2), 3), multiplyInt32.Binary(1, multiplyInt32.Binary(2, 3))); } [TestMethod()] public void ClockTest() { // Stolen from: http://channel9.msdn.com/Shows/Going+Deep/Brian-Beckman-Dont-fear-the-Monads IMonoid<int> clock = 12.Monoid((a, b) => (a + b) % 12); Assert.AreEqual(12, clock.Unit); Assert.AreEqual((7 + 10) % 12, clock.Binary(7, 10)); // Monoid law 1: Unit Binary m == m Assert.AreEqual(111 % 12, clock.Binary(clock.Unit, 111)); // Monoid law 2: m Binary Unit == m Assert.AreEqual(111 % 12, clock.Binary(111, clock.Unit)); // Monoid law 3: (m1 Binary m2) Binary m3 == m1 Binary (m2 Binary m3) Assert.AreEqual(clock.Binary(clock.Binary(11, 22), 33), clock.Binary(11, clock.Binary(22, 33))); } [TestMethod()] public void BooleanTest() { IMonoid<bool> orBoolean = false.Monoid((a, b) => a || b); Assert.IsFalse(orBoolean.Unit); Assert.AreEqual(true || false, orBoolean.Binary(true, false)); // Monoid law 1: Unit Binary m == m Assert.AreEqual(true, orBoolean.Binary(orBoolean.Unit, true)); Assert.AreEqual(false, orBoolean.Binary(orBoolean.Unit, false)); // Monoid law 2: m Binary Unit == m Assert.AreEqual(true, orBoolean.Binary(true, orBoolean.Unit)); Assert.AreEqual(false, orBoolean.Binary(false, orBoolean.Unit)); // Monoid law 3: (m1 Binary m2) Binary m3 == m1 Binary (m2 Binary m3) Assert.AreEqual(orBoolean.Binary(orBoolean.Binary(true, false), true), orBoolean.Binary(true, orBoolean.Binary(false, true))); IMonoid<bool> andBoolean = true.Monoid((a, b) => a && b); Assert.IsTrue(andBoolean.Unit); Assert.AreEqual(true && false, andBoolean.Binary(true, false)); // Monoid law 1: Unit Binary m == m Assert.AreEqual(true, andBoolean.Binary(andBoolean.Unit, true)); Assert.AreEqual(false, andBoolean.Binary(andBoolean.Unit, false)); // Monoid law 2: m Binary Unit == m Assert.AreEqual(true, andBoolean.Binary(true, andBoolean.Unit)); Assert.AreEqual(false, andBoolean.Binary(false, andBoolean.Unit)); // Monoid law 3: (m1 Binary m2) Binary m3 == m1 Binary (m2 Binary m3) Assert.AreEqual(andBoolean.Binary(andBoolean.Binary(true, false), true), andBoolean.Binary(true, andBoolean.Binary(false, true))); } [TestMethod()] public void EnumerableTest() { IMonoid<IEnumerable<int>> concatEnumerable = Enumerable.Empty<int>().Monoid((a, b) => a.Concat(b)); Assert.IsFalse(concatEnumerable.Unit.Any()); int[] x = new int[] { 0, 1, 2 }; int[] y = new int[] { 3, 4, 5 }; EnumerableAssert.AreEqual(concatEnumerable.Binary(x, y), x.Concat(y)); // Monoid law 1: Unit Binary m == m EnumerableAssert.AreEqual(concatEnumerable.Binary(concatEnumerable.Unit, x), x); // Monoid law 2: m Binary Unit == m EnumerableAssert.AreEqual(concatEnumerable.Binary(x, concatEnumerable.Unit), x); // Monoid law 3: (m1 Binary m2) Binary m3 == m1 Binary (m2 Binary m3) EnumerableAssert.AreEqual( concatEnumerable.Binary(concatEnumerable.Binary(x, y), x), concatEnumerable.Binary(x, concatEnumerable.Binary(y, x))); } [TestMethod()] public void NullableTest() { IMonoid<int> addInt32 = 0.Monoid((a, b) => a + b); IMonoid<Nullable<int>> addNullable = addInt32.MonoidOfNullable(); Assert.IsFalse(addNullable.Unit.HasValue); Assert.AreEqual(addInt32.Binary(1, 2), addNullable.Binary(1.Nullable(), 2.Nullable()).Value); Assert.AreEqual(1, addNullable.Binary(1.Nullable(), new Nullable<int>()).Value); Assert.AreEqual(2, addNullable.Binary(new Nullable<int>(), 2.Nullable()).Value); Assert.IsFalse(addNullable.Binary(new Nullable<int>(), new Nullable<int>()).HasValue); // Monoid law 1: Unit Binary m == m Assert.AreEqual(1, addNullable.Binary(addNullable.Unit, 1.Nullable()).Value); // Monoid law 2: m Binary Unit == m Assert.AreEqual(1, addNullable.Binary(1.Nullable(), addNullable.Unit).Value); // Monoid law 3: (m1 Binary m2) Binary m3 == m1 Binary (m2 Binary m3) Nullable<int> left = addNullable.Binary(addNullable.Binary(1.Nullable(), 2.Nullable()), 3.Nullable()); Nullable<int> right = addNullable.Binary(1.Nullable(), addNullable.Binary(2.Nullable(), 3.Nullable())); Assert.AreEqual(left.Value, right.Value); } }