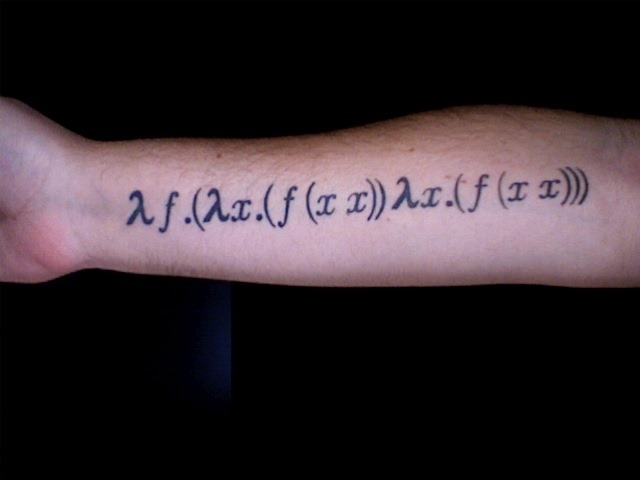Lambda Calculus via C# (7) Fixed Point Combinator and Recursion
[FP & LINQ via C# series]
[Lambda Calculus via C# series]
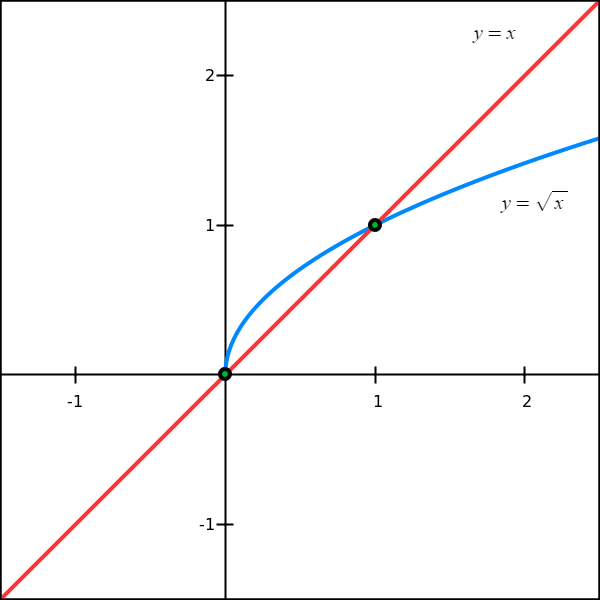
p is the fixed point (aka invariant point) of function f if and only if:
p
≡ f p
Take function Math.Sqrt as example, it has 2 fix point, 0 and 1, so that 0 ≡ Math.Sqrt(0) and 1 ≡ Math.Sqrt(1).
The above fixed point definition also leads to infinite substitution:
p
≡ f p
≡ f (f p)
≡ f (f (f p))
≡ ...
≡ f (f (f ... (f p) ...))
Similarly, the fixed point combinator Y is defined as if Y f is the fixed point of f:
(Y f)
≡ f (Y f)
Normal order fixed point combinator (Y combinator) and recursion
The following Y combinator is an implementation of fixed point combinator, discovered by Haskell Curry:
Y := λf.(λg.f (g g)) (λg.f (g g))
It is called the normal order fixed point combinator:
Y f
≡ (λf.(λg.f (g g)) (λg.f (g g))) f
≡ (λg.f (g g)) (λg.f (g g))
≡ f ((λg.f (g g)) (λg.f (g g)))
≡ f (Y f)
The following is Y implemented in SKI:
Y := S (K (S I I)) (S (S (K S) K) (K (S I I)))
And just in SK:
Y := S S K (S (K (S S (S (S S K)))) K)
When Y f can also be substituted infinitely:
(Y f)
≡ f (Y f)
≡ f (f (Y f))
≡ f (f (f (Y f)))
≡ ...
≡ f (f (f ... (f (Y f)) ...))
So Y can be used to implement recursion. As fore mentioned, in lambda calculus, a function cannot directly apply it self in its body. Take the factorial function as example, the factorial of n is defined recursively:
- If n is greater than 0, then factorial of n is the multiplication of n and factorial of n – 1
- if n is 0, then factorial of n is 1
So naturally:
Factorial := λn.If (n == 0) (λx.1) (λx.n * (Factorial (n - 1)))
However, in lambda calculus the above definition is illegal, because the self reference does not work anonymously:
λn.If (n == 0) (λx.1) (λx.n * (? (n - 1)))
Now with the power of Y combinator, the recursion can be implemented, but still in the anonymous way. First, in above definition, just pass the reference of itself as an variable/argument:
λf.λn.If (n == 0) (λx.1) (λx.n * (f (n - 1)))
If the above function is called FactorialHelper, then the Factorial function can be implemented as:
FactorialHelper := λf.λn.If (n == 0) (λx.1) (λx.n * (f (n - 1)))
Factorial := Y FactorialHelper
So the recursive Factorial is implemented anonymously:
Factorial
≡ Y FactorialHelper
≡ (λf.(λg.f (g g)) (λg.f (g g))) FactorialHelper
≡ (λf.(λg.f (g g)) (λg.f (g g))) (λf.λn.If (n == 0) (λx.1) (λx.n * (f (n - 1))))
When Factorial is applied, according to the definition of Factorial and Y:
Factorial 3
≡ Y FactorialHelper 3
≡ FactorialHelper (Y FactorialHelper) 3
Here (Y FactorialHelper) can be substituted by Factorial, according to the definition. So FactorialHelper is called with Factorial and n, exactly as expected.
The normal order Y combinator does not work with applicative order reduction. In applicative order, here FactorialHelper is applied with (Y FactorialHelper), so the right most argument Y FactorialHelper should be reduced first, which leads to infinite reduction:
FactorialHelper (Y FactorialHelper) 3
≡ FactorialHelper (FactorialHelper (Y FactorialHelper)) 3
≡ FactorialHelper (FactorialHelper (FactorialHelper (Y FactorialHelper))) 3
≡ ...
The normal order Y combinator only works with normal order. In normal order, here FactorialHelper is applied with (Y FactorialHelper), so the left most function FactorialHelper should be reduced first:
FactorialHelper (Y FactorialHelper) 3
≡ (λf.λn.If (n == 0) (λx.1) (λx.n * (f (n - 1)))) (Y FactorialHelper) 3
≡ (λn.If (n == 0) (λx.1) (λx.n * (Y FactorialHelper (n - 1)))) 3
≡ If (3 == 0) (λx.1) (λx.3 * (Y FactorialHelper (3 - 1)))
≡ If (False) (λx.1) (λx.3 * (Y FactorialHelper (3 - 1))
≡ 3 * (Y FactorialHelper (3 - 1))
≡ 3 * (FactorialHelper (Y FactorialHelper) (3 - 1))
≡ 3 * ((λf.λn.If (n == 0) (λx.1) (λx.n * (f (n - 1)))) (Y FactorialHelper) (3 - 1))
≡ 3 * ((λn.If (n == 0) (λx.1) (λx.n * (Y FactorialHelper (n - 1)))) (3 - 1))
≡ 3 * (If ((3 - 1) == 0) (λx.1) (λx.(3 - 1) * (Y FactorialHelper ((3 - 1) - 1))))
≡ 3 * ((3 - 1) * (Y FactorialHelper ((3 - 1) - 1)))
≡ 3 * (2 * (Y FactorialHelper ((3 - 1) - 1)))
≡ 3 * (2 * (FactorialHelper (Y FactorialHelper) ((3 - 1) - 1)))
≡ 3 * (2 * ((λf.λn.If (n == 0) (λx.1) (λx.n * (f (n - 1)))) (Y FactorialHelper) ((3 - 1) - 1)))
≡ 3 * (2 * ((λn.If (n == 0) (λx.1) (λx.n * (Y FactorialHelper (n - 1)))) ((3 - 1) - 1)))
≡ 3 * (2 * (If (((3 - 1) - 1) == 0) (λx.1) (λx.((3 - 1) - 1) * (Y FactorialHelper (((3 - 1) - 1) - 1)))))
≡ 3 * (2 * (((3 - 1) - 1) * (Y FactorialHelper (((3 - 1) - 1) - 1))))
≡ 3 * (2 * (1 * (Y FactorialHelper (((3 - 1) - 1) - 1))))
≡ 3 * (2 * (1 * (FactorialHelper (Y FactorialHelper) (((3 - 1) - 1) - 1))))
≡ 3 * (2 * (1 * ((f.λn.If (n == 0) (λx.1) (λx.n * (f (n - 1)))) (Y FactorialHelper) (((3 - 1) - 1) - 1))))
≡ 3 * (2 * (1 * ((n.If (n == 0) (λx.1) (λx.n * (Y FactorialHelper (n - 1)))) (((3 - 1) - 1) - 1))))
≡ 3 * (2 * (1 * (If ((((3 - 1) - 1) - 1) == 0) (λx.1) (λx.(((3 - 1) - 1) - 1) * (Y FactorialHelper ((((3 - 1) - 1) - 1) - 1))))))
≡ 3 * (2 * (1 * 1))
So the Y f infinite reduction is blocked in in normal order reduction. First, Y f is reduced to f (Y f), then the next reduction is to reduce leftmost expression f, not the the rightmost (Y f). In the above example Y FactorialHelper n:
- If n is greater than 0, Y Factorial n is reduced to n * (Y Factorial (n - 1)), where Y Factorial can be further reduced, so the recursion continues.
- If n is 0, Y Factorial n is reduced to 1. The reduction ends, so the recursion terminates.
Y combinator is easy to implement in C#. Generally, for a recursive function f of type T -> TResult, its helper function accepts the T -> TResult function and a T value, then return TResult, so its helper function is of type (T -> TResult) –> T -> TResult. Y can be viewed as accepting helper function and returns f. so Y is of type ((T -> TResult) –> T -> TResult) -> (T -> TResult). So:
public static partial class FixedPointCombinators<T, TResult> { // Y = (g => f(g(g)))(g => f(g(g))) public static readonly Func<Func<Func<T, TResult>, Func<T, TResult>>, Func<T, TResult>> Y = f => new SelfApplicableFunc<Func<T, TResult>>(g => f(g(g)))(g => f(g(g))); }
Here are the types of the elements in above lambda expression:
- g: SelfApplicableFunc<T -> TResult>
- g(g): T -> TResult
- f: (T -> TResult) –> T -> TResult
- f(g(g)): T => TResult
- g => f(g(g)): SelfApplicableFunc<T -> TResult> –> T -> TResult, which is SelfApplicableFunc<T -> TResult> by definition
- (g => f(g(g)))(g => f(g(g))): T -> TResult
For Factorial, apparently it is of function type Numeral -> Numeral, so FactorialHelper is of function type (Numeral -> Numeral) –> Numeral -> Numeral:
using static FixedPointCombinators<Numeral, Numeral>; public static partial class ChurchNumeral { // FactorialHelper = factorial => n => If(n == 0)(_ => 1)(_ => n * factorial(n - 1)) public static readonly Func<Func<Numeral, Numeral>, Func<Numeral, Numeral>> FactorialHelper = factorial => n => If(n.IsZero()) (_ => One) (_ => n.Multiply(factorial(n.Subtract(One)))); public static readonly Func<Numeral, Numeral> Factorial = Y(FactorialHelper); }
Calling above Factorial always throws StackOverflowException, because in C# executes in applicative order. When Factorial is called, it calls normal order Y in applicative order, which causes infinite execution.
Applicative order fixed point combinator (Z combinator) and recursion
The above Y combinator does not work in C#. When reducing Y f in applicative order, the self application in expression f (g g) leads to infinite reduction, which need to be blocked. The solution is to eta convert f (g g) to λx.f (g g) x. So the applicative order fixed point combinator is:
Z := λf.(λg.λx.f (g g) x) (λg.λx.f (g g) x)
It is called Z combinator. Now reduce Z f in applicative order:
Z f
≡ (λf.(λg.λx.f (g g) x) (λg.λx.f (g g) x)) f
≡ (λg.λx.f (g g) x) (λg.λx.f (g g) x)
≡ λx.f ((λg.λx.f (g g) x) (λg.λx.f (g g) x)) x
≡ λx.f (Z f) x
This time Z f is not reduced to f (Z f), but reduced to the eta expanded version λx.f (Z f) x, so any further reduction is blocked. Still take factorial as example:
Factorial 3
≡ Z FactorialHelper 3
≡ (λx.FactorialHelper (Z FactorialHelper) x) 3
≡ FactorialHelper (Z FactorialHelper) 3
≡ FactorialHelper (λx.FactorialHelper (Z FactorialHelper) x) 3
≡ (λf.λn.If (n == 0) (λx.1) (λx.n * (f (n - 1)))) (λx.FactorialHelper (Z FactorialHelper) x) 3
≡ (λn.If (n == 0) (λx.1) (λx.n * ((λx.FactorialHelper (Z FactorialHelper) x) (n - 1)))) 3
≡ If (3 == 0) (λx.1) (λx.3 * ((λx.FactorialHelper (Z FactorialHelper) x) (3 - 1)))
≡ If (False) (λx.1) (λx.3 * ((λx.FactorialHelper (Z FactorialHelper) x) (3 - 1)))
≡ 3 * ((λx.FactorialHelper (Z FactorialHelper) x) (3 - 1))
≡ 3 * ((λx.FactorialHelper (Z FactorialHelper) x) 2)
≡ 3 * (FactorialHelper (Z FactorialHelper) 2)
≡ 3 * (FactorialHelper (λx.FactorialHelper (Z FactorialHelper) x) 2)
≡ 3 * ((λf.λn.If (n == 0) (λx.1) (λx.n * (f (n - 1)))) (λx.FactorialHelper (Z FactorialHelper) x) 2)
≡ 3 * ((λn.If (n == 0) (λx.1) (λx.n * ((λx.FactorialHelper (Z FactorialHelper) x) (n - 1)))) 2)
≡ 3 * (If (2 == 0) (λx.1) (λx.2 * ((λx.FactorialHelper (Z FactorialHelper) x) (2 - 1))))
≡ 3 * (If (False) (λx.1) (λx.2 * ((λx.FactorialHelper (Z FactorialHelper) x) (2 - 1))))
≡ 3 * (2 * ((λx.FactorialHelper (Z FactorialHelper) x) (2 - 1)))
≡ 3 * (2 * ((λx.FactorialHelper (Z FactorialHelper) x) 1))
≡ 3 * (2 * (FactorialHelper (Z FactorialHelper) 1))
≡ 3 * (2 * (FactorialHelper (λx.FactorialHelper (Z FactorialHelper) x) 1))
≡ 3 * (2 * ((λf.λn.If (n == 0) (λx.1) (λx.n * (f (n - 1)))) (λx.FactorialHelper (Z FactorialHelper) x) 1))
≡ 3 * (2 * ((λn.If (n == 0) (λx.1) (λx.n * ((λx.FactorialHelper (Z FactorialHelper) x) (n - 1)))) 1))
≡ 3 * (2 * (If (1 == 0) (λx.1) (λx.1 * ((λx.FactorialHelper (Z FactorialHelper) x) (1 - 1)))))
≡ 3 * (2 * (If (False) (λx.1) (λx.1 * ((λx.FactorialHelper (Z FactorialHelper) x) (1 - 1)))))
≡ 3 * (2 * (1 * ((λx.FactorialHelper (Z FactorialHelper) x) (1 - 1))))
≡ 3 * (2 * (1 * ((λx.FactorialHelper (Z FactorialHelper) x) 0)))
≡ 3 * (2 * (1 * (FactorialHelper (Z FactorialHelper) 0)))
≡ 3 * (2 * (1 * (FactorialHelper (λx.FactorialHelper (Z FactorialHelper) x) 0)))
≡ 3 * (2 * (1 * ((λf.λn.If (n == 0) (λx.1) (λx.n * (f (n - 1)))) (λx.FactorialHelper (Z FactorialHelper) x) 0)))
≡ 3 * (2 * (1 * ((λn.If (n == 0) (λx.1) (λx.n * ((λx.FactorialHelper (Z FactorialHelper) x) (n - 1)))) 0)))
≡ 3 * (2 * (1 * (If (0 == 0) (λx.1) (λx.0 * ((λx.FactorialHelper (Z FactorialHelper) x) (n - 1))))))
≡ 3 * (2 * (1 * (If (True) (λx.1) (λx.0 * ((λx.FactorialHelper (Z FactorialHelper) x) (n - 1))))))
≡ 3 * (2 * (1 * 1))
In C#, Z combinator can be implemented in the same pattern. Just eta expand f(g(g)) to x => f(g(g))(x):
public static partial class FixedPointCombinators<T, TResult> { // Z = (g => x => f(g(g))(x))(g => x => f(g(g))(x)) public static readonly Func<Func<Func<T, TResult>, Func<T, TResult>>, Func<T, TResult>> Z = f => new SelfApplicableFunc<Func<T, TResult>>(g => x => f(g(g))(x))(g => x => f(g(g))(x)); }
The types of the elements in above lambda expression are the same as in Y combinator, and x is of type T.
Now Factorial can be defined with Z and above FactorialHelper:
using static ChurchBoolean; using static FixedPointCombinators<Numeral, System.Func<Numeral, Numeral>>; public static partial class ChurchNumeral { // DivideByHelper = divideBy => dividend => divisor => If(dividend >= divisor)(_ => 1 + divideBy(dividend - divisor)(divisor))(_ => 0) private static readonly Func<Func<Numeral, Func<Numeral, Numeral>>, Func<Numeral, Func<Numeral, Numeral>>> DivideByHelper = divideBy => dividend => divisor => If(dividend.IsGreaterThanOrEqualTo(divisor)) (_ => One.Add(divideBy(dividend.Subtract(divisor))(divisor))) (_ => Zero); public static readonly Func<Numeral, Func<Numeral, Numeral>> DivideBy = Z(DivideByHelper); }
Another recursion example is Fibonacci number. The nth Fibonacci number is defined recursively:
- if n is greater than 1, then the nth Fibonacci number is the sum of the (n -1)th Fibonacci number and the (n -2)th Fibonacci number.
- if n is 1 or 0, then the nth Fibonacci number is n
So naturally:
Fibonacci := λn.If (n > 1) (λx.(Fibonacci (n - 1)) + (Fibonacci (n - 2))) (λx.n)
Again, the above recursive definition is illegal in lambda calculus, because the self reference does not work anonymously:
λn.If (n > 1) (λx.(? (n - 1)) + (? (n - 2))) (λx.n)
Following the same helper function pattern as FactorialHelper, a FibonacciHelper can be defined to pass the Fibonacci function as a variable/argument, then Fibonacci can be defined with Z and FibonacciHelper:
FibonacciHelper := λf.λn.If (n > 1) (λx.(f (n - 1)) + (f (n - 2))) (λx.n)
Fibonacci := Z FibonacciHelper
Now Fibonacci is recursive but still can go anonymous, without any self reference:
Fibonacci
≡ Z FibonacciHelper
≡ (λf.(λg.λx.f (g g) x) (λg.λx.f (g g) x)) FibonacciHelper
≡ (λf.(λg.λx.f (g g) x) (λg.λx.f (g g) x)) (λf.λn.If (n > 1) (λx.(f (n - 1)) + (f (n - 2))) (λx.n))
In C#:
// FibonacciHelper = fibonacci => n => If(n > 1)(_ => fibonacci(n - 1) + fibonacci(n - 2))(_ => n) private static readonly Func<Func<Numeral, Numeral>, Func<Numeral, Numeral>> FibonacciHelper = fibonacci => n => If(n.IsGreaterThan(One)) (_ => fibonacci(n.Subtract(One)).Add(fibonacci(n.Subtract(Two)))) (_ => n); // Fibonacci = Z(FibonacciHelper) public static readonly Func<Numeral, Numeral> Fibonacci = Z(FibonacciHelper);
Previously, in the Church numeral arithmetic, the following illegal DivideBy with self reference was temporarily used:
DivideBy := λa.λb.If (a >= b) (λx.1 + (DivideBy (a - b) b)) (λx.0)
Finally, with Z, an legal DivideBy in lambda calculus can be defined, following the same helper function pattern:
DivideByHelper := λf.λa.λb.If (a >= b) (λx.1 + (f (a - b) b)) (λx.0)
DivideBy := Z DivideByHelper
The following is the formal version of DivideBy:
DivideBy
≡ Z DivideByHelper
≡ (λf.(λg.λx.f (g g) x) (λg.λx.f (g g) x)) DivideByHelper
≡ (λf.(λg.λx.f (g g) x) (λg.λx.f (g g) x)) (λf.λa.λb.If (a >= b) (λx.1 + (f (a - b) b)) (λx.0))
In C#:
// DivideByHelper = divideBy => dividend => divisor => If(dividend >= divisor)(_ => 1 + divideBy(dividend - divisor)(divisor))(_ => 0) private static readonly Func<Func<Numeral, Func<Numeral, Numeral>>, Func<Numeral, Func<Numeral, Numeral>>> DivideByHelper = divideBy => dividend => divisor => If(dividend.IsGreaterThanOrEqualTo(divisor)) (_ => One.Add(divideBy(dividend.Subtract(divisor))(divisor))) (_ => Zero); // DivideBy = Z(DivideByHelper) public static readonly Func<Numeral, Func<Numeral, Numeral>> DivideBy = Z(DivideByHelper);
The following are a few examples
public static partial class NumeralExtensions { public static Numeral Factorial(this Numeral n) => ChurchNumeral.Factorial(n); public static Numeral Fibonacci(this Numeral n) => ChurchNumeral.Fibonacci(n); public static Numeral DivideBy(this Numeral dividend, Numeral divisor) => ChurchNumeral.DivideBy(dividend)(divisor); } [TestClass] public partial class FixedPointCombinatorTests { [TestMethod] public void FactorialTest() { Func<uint, uint> factorial = null; // Must have to be compiled. factorial = x => x == 0 ? 1U : x * factorial(x - 1U); Assert.AreEqual(factorial(0U), 0U.Church().Factorial().Unchurch()); Assert.AreEqual(factorial(1U), 1U.Church().Factorial().Unchurch()); Assert.AreEqual(factorial(2U), 2U.Church().Factorial().Unchurch()); Assert.AreEqual(factorial(8U), 8U.Church().Factorial().Unchurch()); } [TestMethod] public void FibonacciTest() { Func<uint, uint> fibonacci = null; // Must have. So that fibonacci can recursively refer itself. fibonacci = x => x > 1U ? fibonacci(x - 1) + fibonacci(x - 2) : x; Assert.AreEqual(fibonacci(0U), 0U.Church().Fibonacci().Unchurch()); Assert.AreEqual(fibonacci(1U), 1U.Church().Fibonacci().Unchurch()); Assert.AreEqual(fibonacci(2U), 2U.Church().Fibonacci().Unchurch()); Assert.AreEqual(fibonacci(8U), 8U.Church().Fibonacci().Unchurch()); } [TestMethod] public void DivideByTest() { Assert.AreEqual(1U / 1U, 1U.Church().DivideBy(1U.Church()).Unchurch()); Assert.AreEqual(1U / 2U, 1U.Church().DivideBy(2U.Church()).Unchurch()); Assert.AreEqual(2U / 2U, 2U.Church().DivideBy(2U.Church()).Unchurch()); Assert.AreEqual(2U / 1U, 2U.Church().DivideBy(1U.Church()).Unchurch()); Assert.AreEqual(8U / 3U, 8U.Church().DivideBy(3U.Church()).Unchurch()); Assert.AreEqual(3U / 8U, 3U.Church().DivideBy(8U.Church()).Unchurch()); } }