Why complexity metrics don´t yet help ease software maintenance

Jeroen van den Bos bemoaned in a recent post, of how little help automatic software architecture complexity  metrics are to him when assessing effort of a software change. I feel with Jeroen and think, we need to take another look at what complexity means (for software development). Roger Sessions took at stab at this in his article "A Better Path to Enterprise Architecture" - but I disagree with him in some regards.

So, what is complexity about? Why should we care? I like to think of it as a measure for how hard it is to know what impact a change will have on a system. If something is complicated, it´s hard to understand. But if something is complex, it´s hard to manipulate. Since software needs to be understood as well as changed, it should not be more complicated or more complex than necessary. That´s why we should care.

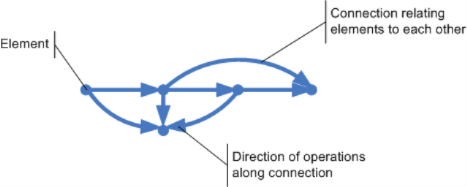
Now, what is it, that can be more or less complex? Complexity is an attribute of systems. And a system is a mesh of elements related to each other:

Elements without any relation to each other, do not constitute a system. They are just a set of elements. But once the elements are connected in some way, a system exists. From a system´s point of view, the elements are even quite neglible. They are black boxes, since the system´s main constituent are the connections and the operations running along those connections. Without connections and operations no system!

Note: To me, software is a system (see my blog series for details (sorry, it´s all German)). It´s a system of so called swolons (short for software holon) on different logical levels of abstraction and manifested in physical artifacts of different "size". Modules (logical units of code), methods/subroutines, types, type instances, assemblies, components, AppDomains, processes: they are all swolons. Swolons are the elements of the system "software" in general.

Elements and operations along connection are not enough to create complexity, though. If they were, then complexity would rise with more elements and more connections. However, more elements and connections alone to me just make a system more complicated. Elements (vertices) and connections (edges) are static. They define the structure/topology of a graph, nothing more.

But complexity has a different quality. Complexity is about dynamics, about change. And change means moving from one state to another. So the notion missing from the picture so far is: state. The state of a system is the sum of the states of its elements.

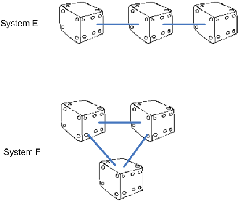
But it´s not as easy as Roger Sessions depicts it in his article. He claims, a coin and a dice were systems, and a dice was more complex than a coin (see figure below), because a dice has more potential states (6) than a coin (2).

Source: Microsoft

But are coin and dice systems at all? As he depicts them, I´d say no. Where are the elements of the systems? Or if you take a coin as an element, where are the others and where are the connections between the elements?

To Roger, complexity is synonymous with "number of states". That´s why he continous his argument by saying, a "system" of three dice was more complex than just one dice, because it can assume 6*6*6=216 different states.

I, however, don´t think just taking three dice instead of one leads to a more complex system for the simple reason that there is no connection between the three dice. One coin, one dice, three dice... it´s all the same complexity wise. A dice with its 6 states might be more complicated than a coind with its 2 states, and three dice might be more complicated than a single dice. But they all should not be called systems. And I think a single "super dice" with 216 faces would be as complicated as three regular dice.

In order to really start talking about systems, any number of coins or dice need to be connected like in the below figure:

Source: My German Blog

Of course such connections would not make any difference with regard to the number of states. Rather they would make all the difference with regard to changing the state of the system. Because what happens, if I change the state in Roger´s "system" of three non-connected dice? Nothing much. The state of the "system" changes absolutely predictably. If the top face of the dice were 3 and 5 and 1 and thus the "system´s" state 351 and I turn the first dice around, the "system´s" state becomes 451. There is no doubt about it, no hesitation in my thinking, it´s crystal clear to me what will be the state of the "system" after changing state of just one of its elements.

But what if the elements/dice are connected? What if there was a real system like in the above figure? There system E´s state is 222. But what will the system´s state be if I turn the first dice around? Will it really be 522? Maybe, maybe not. It depends on its relation with the second dice. Maybe this relation is a loose one, maybe both dice are connected by just a thin thread. Then turning the first dice probably does not cause the second one to turn too.

But maybe the dice are both connected by a spring. Then turning the first dice surely would affect the state of the second dice. Maybe in a very easy to understand way (e.g. turning the first dice just turns the second, too; 222 would then become 552), but maybe in a not so easy to understand way (e.g. if dice 1 shows an even number before the turn, then the second dice is not turned, otherwise it is; 222 would then become 522, and only with a second turn of dice 1 also dice 2 would turn leading to 252).

A system´s complexity thus is a matter of dependencies between the elements´ states. System complexity is a function of the coupling of the elements along the their relations. To assess the complexity of a system, not only the number of elements and their connections need to be known, but also the "tightness" or "strength" of those connections as well as the direction in which state changes flow along them.

With that in mind back to Jeroen´s trouble with current software architecture complexity metrics. First we need to clarify what we´re talking about: a system of swolons at design time. I think that´s important to note. Swolons as units of code with functionality and state exist in two "realms": design time and runtime. An object clearly is a runtime swolon. It´s class, though, is a design time swolon.

The interesting thing, now, is, state changes flow differently at design time and runtime. At runtime the state of a swolon is made up of its data. State changes in a swolon are induced by messages received by that swolon. Message senders (clients) cause state changes in message receivers (services) - unless a service swolon is stateless. (Returning a result from a service to a client requires both to change their roles; client and service would be connected by a bidirectional relation.) Messages are the operations of runtime systems. Only where messages flow between swolons there is a system at all.

What´s the state of swolons at design time, though? Classes are prototypical design time swolons. But what´s their state at design time? Source code is the design time state of a design time swolon. And the operations along the dependency relations between clients and services are source code modifications.

However, modifications mostly (often?) flow in the opposite direction of a dependency: it is more likely that a client´s source code needs to change if it´s service changes than the other way around - I´d say. But of course, changes in a client might require changes to one of its services.

This all still might seem easy - but what if there are not just 2 or 10 swolons, but 100 or 1000? How many connections are there between them? But most importantly: How do changes to one swolons data (runtime) or one swolons source code (design time) affect other swolons?

I don´t think the real impact of such changes can be calculated yet by any tool for at least three reasons:

• State changes depend on the initial cause. Changing the same swolon in different ways might cause waves of changes of different size rippling through the mesh of connected swolons.
• The same cause might lead to different waves of changes depending on the previous state.
• The tightness of the coupling between swolons is not so much a matter of quantity (e.g. number of connections), but rather a matter of quality. And I don´t know how to assess that automatically. It´s beyond counting anything, it has to do with the meaning of the code, its purpose.

This leads me to the conclusion: Trying to calculate the complexity of a software is a vain effort. From the number of elements and their basic connections only a rough approximation of a system´s complexity can be derived. Complexity is not absolute, but depending on the cause. At best it can only be assessed for a class of causes, I´d say.

So if you want to know the complexity of your software to get a better idea of how much maintenance will cost you... you first need to classify the changes that might need to be applied to the design time swolons constituting the software system. Then you need to "calculate" how far reaching the effects of changes according to those classes would be in the mesh of interconnected swolons.

My bottom line thus is: Do whatever you can to limit the effect of state changes in swolons to keep the complexity of your software system low. Decoupling is one measure in that regard, black box thinking (and code organization) is another measure. Put up "firewalls" between swolons (at design time) so as to hold off changes on one side of it from affecting the other side.

Roger Sessions recommends partioning - and I agree with him. He just does not explain it well. The term "decoupling" does not appear in his article. But what he means is: Partion groups of swolons so that they are as loosely coupled as possible (or not at all); then changes to one such group won´t be able to set another group "on fire". Well, that surely is a very valuable timeless advice.