Adventures in F# - F# 101 Part 5 (Pattern Matching)
Where We Are
Before we begin today, let's catch up to where we are today:
- Part 1 - Basic functional programming
- Part 2 - Currying and Tuples
- Part 3 - Scope, Recursion and Anonymous Functions
- Part 4 - History of F#, Operators and Lists
- Pattern Matching
- Active Patterns
One of the interesting and more powerful features of the F# language is Pattern Matching. Don't be tempted to think of them as simple switch statements as they are much more powerful than that. Pattern matching is used to test whether the piece under test has a desired state, find relevant information, or substitute parts with other parts. Most functional languages such as Haskell, ML, and OCaml have them, and F# is no exception to its support.
At first glance, like I said, you might be tempted to think of them as the C# switch statement. But, this is more powerful as you can have ranges support, can case on .NET types and plenty of other things you cannot do in other .NET languages. Let's walk through a simple example of the old Fibonacci sequence that I've shown in the past. But this time, I'll walk through it several times as I make improvements each iteration by adding more features to support failover, etc.
In order to use pattern matching with explicit values, you can use the match and with keywords. This allows you to match a particular parameter with the following conditions.
#light
let rec fib n =
match n with
| 0 -> 1
| 1 -> 1
| x -> fib(n - 2) + fib(n - 1)
print_any (fib (-1))
Ok, so what we have here is a simple one with pattern matching which checks for a 0, then a 1, and then the default case goes to do the Fibonacci sequence calculation. The other two would be considered escape clauses for the last calculation. But, we can do better than this. Let's try again by compacting it just a little.
#light
let rec fib n =
match n with
| 0 | 1 -> 1
| x -> fib(n - 2) + fib(n - 1)
print_any (fib (-1))
Now the code is a bit more compact as we can combine two values on one line as you can see. But, we haven't hit a fail case if the value is less than 0. That's not a good thing. Luckily F# gives us a failure function to deal with something like this. We can use the when clause if we want to check for ranges. Also, we can specify that the condition is a failure with the failwith keyword. Let's now walk through the more complete scenario.
#light
let rec fib n =
match n with
| x when x < 0 -> failwith "value must be greater than or equal to 0"
| 0 | 1 -> 1
| x -> fib(n - 2) + fib(n - 1)
print_any (fib (-1))
And sure enough when you run the program through the debugger, you get the nice picture that tells you of the exact error. It fails with a FailureException and our message shows up as well.
What I always like to do in situations such as these is to look through .NET Reflector to look at how it might show up if it were rendered in C#.
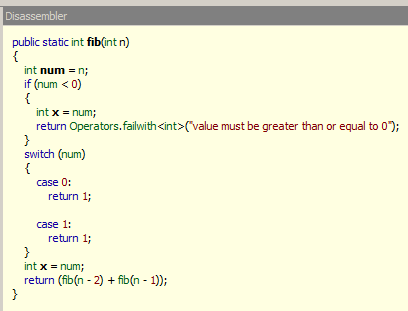
Pretty simple as it uses the switch statements when it can, and then uses the failure outside of it. As you can see, the F# is much cleaner and more to the point than this stuff. Jacob Carpenter took it to a different level though in C# when he went through Generics and Lambda abuse to reproduce the same actions. You can read more about that here.
But, that's easy stuff that can be easily done by C#, albeit differently. Let's try for matching against .NET types instead, which is something C# cannot do via the switch statement. So, in a words, you can definitely tell that it's a bit more powerful than just a simple C# switch statement.
#light
let stringType (t : ob) =
match t with
| :? System.Boolean -> "Boolean"
| :? System.Byte -> "Byte"
| :? System.Int32 -> "Int32"| :? System.Double -> "Double"
| _ -> "Unknown"
print_string (stringType (box 14uy))
print_string (stringType (box false))
print_string (stringType (box "Foo"))
What the above example does is check for the corresponding .NET types by using the :? operator especially reserved for this behavior. Also, note the use of the underscore "_" as a wildcard approach to this. Let's take a look at the results in .NET Reflector again to see what the results look like. Again, it's nothing spectacular just yet.

Let's look at yet another sample when calling a recursive function. This time, let's concatenate a few strings together from an F# list. This is a pretty simple example of using pattern matching to tell when to stop adding onto the existing string.
#light
let stringList = ["foo"; "bar"; "foobar"; "barfoo"]
let rec concatStringList = function
| head :: tail -> head + concatStringList tail
| [] -> ""
print_string (concatStringList stringList)
So, what we're doing is while we have a value to concatenate onto the tail, then add it to the list, else if it's an empty list, let's return a blank string. The keywords head and tail are actually built into the F# language as part of F# lists. The head is the head value on the list, in our case, a string. The tail represents the rest of the list. What's really cool is that ideas from functional programming can actually help your C# and imperative code thinking. We'll get into at a later time... Anyways, I'm always curious what that looks like in Reflector and how it gets translated into C#-ese.

You can also match over two or more parameters as well. This is especially interesting if wanting to cover all variations of a particular combination without messy C# if statements. Let's take a look at matching over a tuple whether we allow a URL to be accessed or not:
#light
let allowUrl url port =
match (url, port) with
| "http://www.microsoft.com/", 80 -> true
| "http://example.com/", 8888 -> true
| _, 80 -> true
| _ -> false
let allowMicrosoft = allowUrl "http://www.microsoft/" 80
printfn "%b" allowMicrosoft
What seems like simple code is actually quite squirrley if you want to translate this into C#. As you can see from the above code, if we pass in the Microsoft address and 80, we can return a true value, else look at the other conditions and if all else fails, then we return false. But, let's take a look at how it's translated into C#.

Definitely handled very elegantly in our F# code as it's one of the strengths. With C#, not as much as you can see from this pretty ugly code that it represents. Matching against enums is pretty easy as well with very little coding effort such as this:
#light
let calcRateByDay (day:System.DayOfWeek) =
match day with
| System.DayOfWeek.Monday -> 0.42
| System.DayOfWeek.Tuesday -> 0.67
| System.DayOfWeek.Wednesday -> 0.56
| System.DayOfWeek.Thursday -> 0.34
| System.DayOfWeek.Friday -> 0.78
| System.DayOfWeek.Saturday -> 0.92
| System.DayOfWeek.Sunday -> 0.18
| _ -> failwith "Unexpected enum value"
print_any (calcRateByDay System.DayOfWeek.Monday)
So, just wrapping up this section for now, as you can notice, we can do all sorts of things with pattern matching and I've barely scratched the surface of it. I won't begin to cover things as pattern matching over unions just yet until I get to that section where I want to talk about them exclusively.
Active Patterns
Now that we understand how pattern matching works, let's take this to a different level. These active patterns allow you to create a union type of various .NET classes and match against them. Unfortunately, Robert Pickering couldn't fit the active patterns into his Foundations of F# book, so you can go ahead instead and read about them here. Also, Luis Diego Fallas posts about them here as well.
To give you a brief sample of what one looks like, let's look through a sample of whether we're looking through files or directories.
#light
let (|File| Directory|) (fileSysInfo : System.IO.FileSystemInfo) =
match fileSysInfo with
| :? System.IO.FileInfo as file -> File (file.Name)
| :? System.IO.DirectoryInfo as dir -> Directory (dir.Name, { for x in dir.GetFileSystemInfos() -> x })
| _ -> assert false
What this allows us to do work with Files as tree structures. You can also use these to walk XML documents and so on. Read the above samples to get more information about them.
Conclusion
Pattern Matching to me is one of the most fundamental pieces to F# and functional programming as a whole. What I've started you with are some basic samples, but these can be applied to binary trees, complex objects and so on. I hope to cover more scenarios soon, and until next time...
